Ben Zenker

I worked intermittently on this project across 6 years of my life, however, only about 6 months within that timeframe was spent writing code. My original inspiration many years ago came from losing my college discount on certain creative tools.

Wiggle Animate is free and open-source, meant to enable creators with access to a powerful tool directly in their web browser.

I released it officially, for all the world to use, in February of 2024.

Wiggle Animate is part of a larger body of work that I've branded as a suite of purpose-built tools that are simple in their feature-set but powerful in what they create. I call these the Wiggle Tools.

https://wiggle.tools/

Why did I feel compelled to build this suite of tools?

I love digital graphics. I spent at least a decade producing/editing videos. My unique degree mixes TV/Film, Technology, and Imaging Science. I worked in Visual Effects, developing plugins & scripts for a handful of media industry tools. I get excited reading about video codecs. I'm genuinely passionate about building great creative tools.

Here is an incredibly simple animation made with the current version of Wiggle Animate. There is much more that can be created with this tool, so I suggest you check it out for yourself!

Built a web-based vector animation application, with custom drawing functionality using the HTML Canvas API. Managed data using MobX and an object-oriented design, with a React front end.

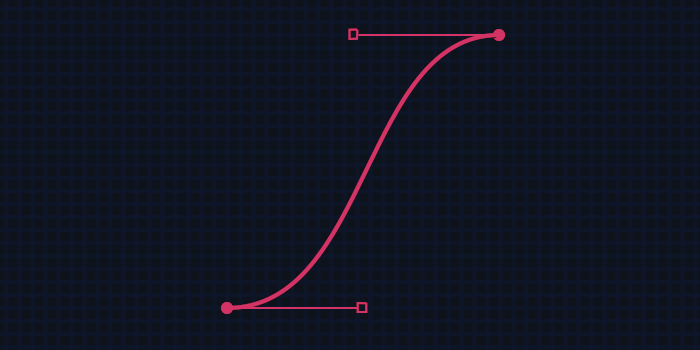
Science, or more specifically mathematics, is at the core of every vector shape and every frame of animation, making it very relevant in the architecture of MicroGraph. What I'd like to highlight is how a Bézier curve, which is often used to represent the vector between two points in 2d space, is also an incredible tool in producing smooth and realistic animations in the 4th dimension, time.

The math that makes it possible to define a curve with 4 points is pretty ingenious, but it's only one of the infinite types of Bézier curves (cubic). You can dive deeper into this topic and play with them visually on this website.

Unfortunately, the general formula defines the curve as a function of how far along the curve you have traveled, which is very different than a traditional x-y series.

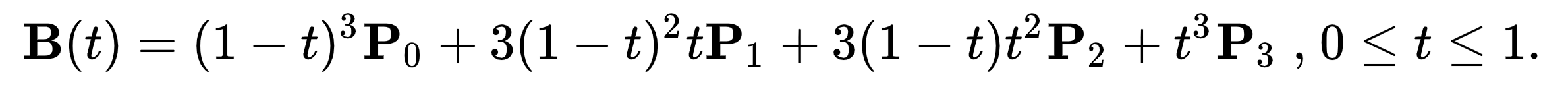
Therefore, to use the beautiful shape of a Bézier curve to define the interpolation between two keyframes, we have to solve the curve so that it can be defined in an x & y relationship, or in this case time & interpolated value.

As you might have read in the code section of this project, I've opted for relative values in every way possible. This holds with keyframe interpolation. With both time and value now normalized on a scale of 0 to 1, we can say that P0 and P3 (the first and last points), will always fall at 0,0 and 1,1.

This gives us the power to greatly reduce the complexity in the function, which saves computation time, and eliminates the possibility of imaginary roots existing for a curve. It puts the emphasis, both mathematically and user experience wise, on the handles of the curve -- which are ultimately what define the smoothness and realisticness of an animation.